株価や為替レートなどのチャート分析で行 われる半値水準の計算の多くが「単純に
高値と安値を足して2で 割る」等差数列的な考え方によって計算されています。
こ れに対してこのアプリは、変化率で計算したときにどの水準が「高値と安値の中
心点」であるか?を計算するもので、等比数列における中 心点を簡単に計算するた
めのツールです。
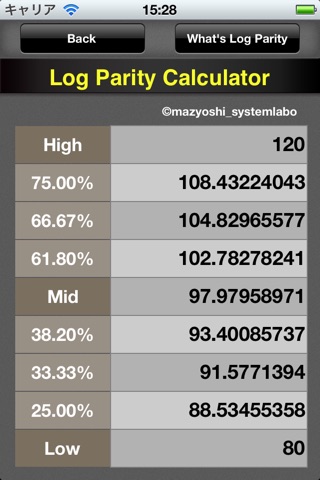
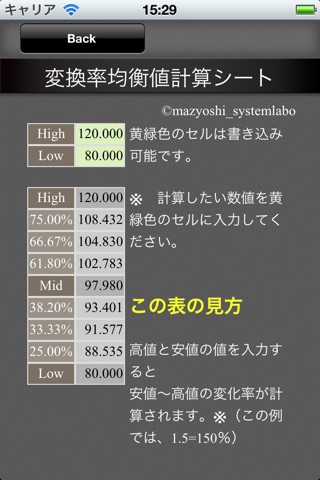
Ratioの 項目をデフォルトの50%としたまま、高値と安値の値を入れるだけで変化率
ベー スの中心点(価格)が表示されます。
計 算方法は「高値÷安値」で得られる「高値は安値の何倍になっているか」の値を
計算し、その値の平方根をとって安値に掛けたものを中心 点として返す仕様となっ
ています。
こ のときRetioを25% として計算すると半分の半分の値を示し、33.33% とすると3
分割した時の値を返すものです。
※Ratio50%=1/2と は、「高値÷安値」で得られた値の平方根=1/2乗 を安値の値
に掛けたものを計算し、Ratio33.33%=1/3と は「高値÷安値」で得られた値の立方
根=1/3乗 を安値の値に掛けたものを計算するという意味です。
『変化率ベースで計算すべき理由』
為替レートや株価における価格の変化の絶 対額だけ捉えて比較してみてもあまり大
きな意味はありません。
1単 位あたり50円の上昇といっても、1000円 の株価の50円の上昇と100円 の株価
の50円の上昇ではその意味合い(価値)は変わってくるからで す。
なぜ、 この意味合いが異なるかを厳密に考えると、50円 変化するその前の基準点が
大きく異なっているから問うことは言うまでもないでしょう。
異 なる銘柄間の比較では、このことはよく自覚されていますが、同じ銘柄において
も、値段が安かったものが上昇し、基準とすべき位置が大 きく変わってしまった時
も、全く同じ事が言えるのですが、明確にこの調整を行っている方は現在のところ少
ないようです。
この同一銘柄の基準点の位置が変わったことを考慮して比較するには、やはり変化
率で考 えることが必須なのです。
『例を上げて説明します。』
100円と200円 の半値はいくら?と言われた時に、簡単なチャート分析手法しか知ら
ないと答えは150円 ということになるでしょう。
この150円 とは算術平均であり、等差数列で考えたときの100円 と200円の中心値
ということになります。
これを変化率(等比数列)の視点で考える と次のようになります。
100円 の価格のものが50%上昇すると100×1.5で150円 となります。
この150円 まで上昇した価格がさらに50%上昇するしたときの値は200円 ではないこ
とは、もう、すぐにおわかりいただけると思います。
150×1.5を 計算した時の答えは、225円で、200円 より25円高い値となります。
※元々あった100円 の50%増加に加え、150円 になる時に増加した50円に対しても
50% 増加した=さらに25円増えたということを考慮しているわけです。 この事を
言い換えると、複利の効果も勘案して計算しているのが変化率ベースで考えていると
いうことになります。
このことは、100円と225円 の変化率ベースでの中心点が150円という事を導きます。
このことから、100円 と200円の変化率ベースでの(複利効果を考慮した)中心点
は、 この例でとりあえず持ちだしてきた150円 よりも低いところにあることがわか
りますね。
それを踏まえて、以下、計算方法を解説します。
さて、100円 が200円に変化した変化率は2.0で す。
2回 同じ変化率で価格が上昇し2倍になったのですから、同じ変化率きっかり2回
で、2になった元の変化率を(1+r) と置くと、
(1+r)×(1+r)= (1+r)2 =2.0
となるような(1+r) をもとめれば良いわけですから、
その値(1+r) は2の平方根(=2^0.5) を計算すれば求められます。
ルート2は1.41421356・・・ ですから100にこれを掛けた
141.423156・・・ が
変化率ベースでの100円 と200円の中心点と考えることが出来るのです。